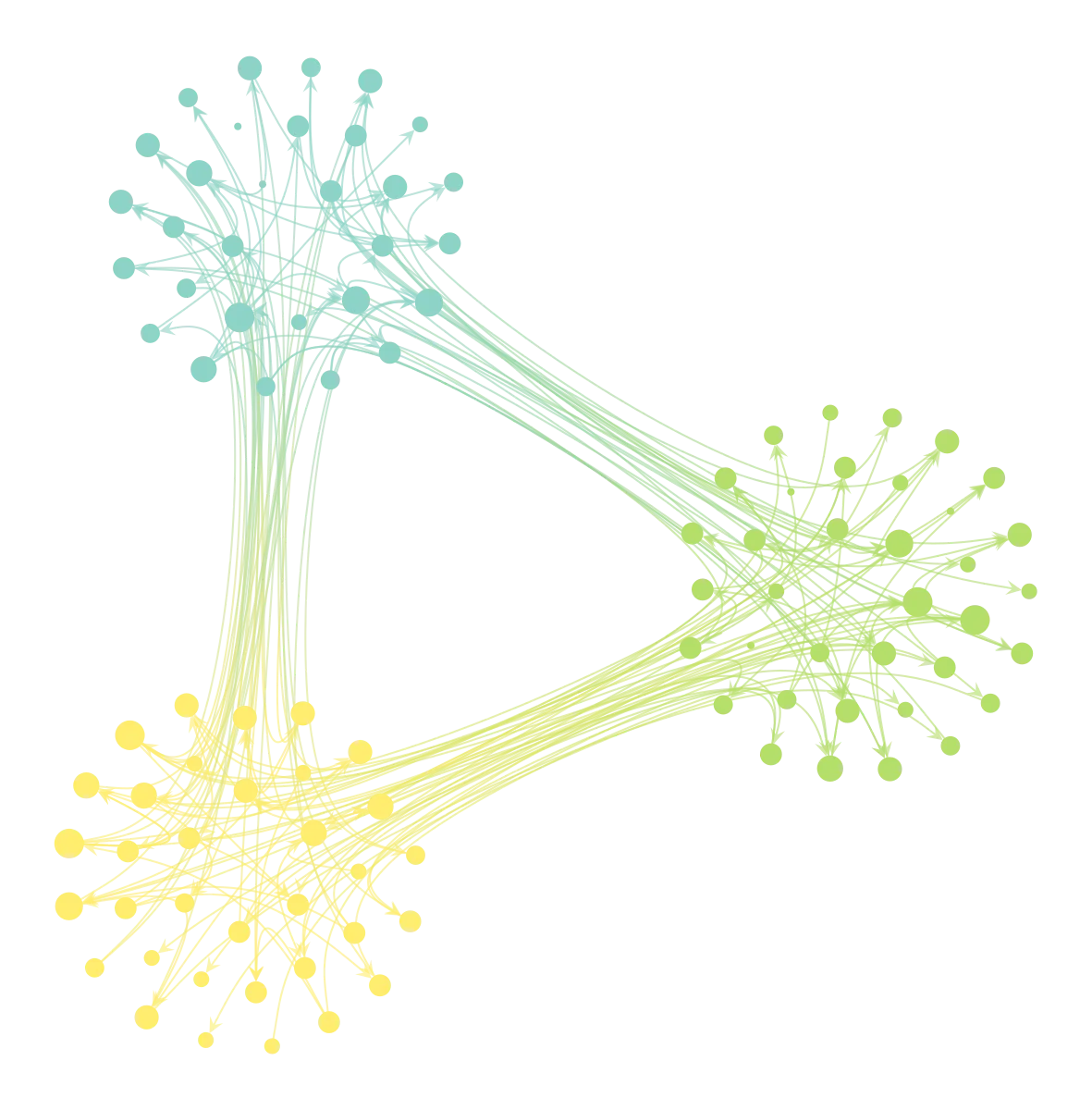
Growing networks with a given assortativity coefficient

Social interaction tends to happen primarily within groups: people usually talk, befriend, and mate mostly with others similar to themselves. Network scientists call this tendency assortativity, which in practice is often measured using a statistic called Newman’s assortativity coefficient $r$ (Newman 2003).¹

Given a network divided into distinct social groups, define $e_{ij}$ as the fraction of edges connecting nodes from group $i$ to group $j$. By construction, we have that $\sum_{i,j} e_{ij}=1$. Further, let $a_i=\sum_j e_{ij}$ represent the fraction of all edge endpoints attached to group $i$, and similarly $b_j=\sum_i e_{ij}$, which equals $a_j$ for undirected networks. Newman’s assortativity coefficient is then given by:

This quantity can be interpreted as a normalized correlation coefficient that ranges from $r=-1$ (fully disassortative), through $r=0$ (no assortativity, random mixing), up to $r=1$ (fully assortative). It is a descriptive statistic that summarizes the group interactions in a given network.²

When setting up generative agent-based models (ABMs) to study social networks, we can thus describe a posteriori the degree of assortative mixing $r$ present in each sampled network; viewed that way, the ABM outputs samples of $r$ via intermediate $e$‘s.

Controlling $r$

But what if we want to set the degree of assortativity in our simulations a priori? This is a common situation in ABMs; we’d like a simple knob to set $r$ and use it as an input to control network generation on the fly. This enables us to study the influence of assortativity $r$ on some other metric of interest $f(r)$. As a concrete example, Binder et al. (2022) find from U.S. Census data that the prevalence of interracial marriages strongly correlates with intergenerational social mobility. To study whether there is a causal connection, we could design an ABM with input $r$ (the assortativity of marriage interactions between races, where each race is a group) and output $f(r)$ (some measure of intergenerational social mobility).

So how do we generate networks with prescribed values of $r$? Since ABMs are typically grown dynamically (edges are added or removed in time steps), we’d like an algorithm that produces networks that converge in time to a some given value of $r := r^*$. More importantly, however, there are many different ways to do this (just think of the many different ways Nature produces assortative structure). We face design choices. What is the simplest possible way, without making unwarranted assumptions or imposing additional biases?

Well, the definition of $r(e)$ given above assumes only the existence of groups with an edge fraction $e$ matrix that makes sense for our problem, so we start there. There are various algorithms for growing networks that converge to a given $e$,³ but we don’t know $e$, only the projection $r(e)$, and there are many $e$-matrices that project down to the same value of $r(e)$. If we can select “the least biased one”, call it $e^*$, a practical and defensible solution to our problem presents itself:

given the target $r^*$, use any algorithm to grow a baby network towards that “least biased” $e^*$ that gives rise to $r^* = r(e^*)$, and we have generated a network with a prescribed value of $r$.

Choosing $e^*$

A natural criterion for choosing $e^*$ comes from the principle of maximum entropy (ME) which dictates how to update probability assignments under newly received information (Jaynes 2003; Knuth and Skilling 2012; Giffin 2009). We can indeed interpret the edge fractions as probabilities⁴ such that $e_{ij}$ specifies a probability mass distribution with two-dimensional index $i,j$. Then it is a well known result that we can impose the assortativity constraint in the minimum constraining way possible — i.e., maximally noncomittal and minimally biased — by using the ME principle. This says that

given the target $r^*$, we should choose out of all possible distributions $e$ that one distribution $e^*$ which has simultaneously maximum entropy and satisfies $r(e^*) = r^*$ together with the normalization requirement $\sum_{ij} e_{ij} = 1$.⁵

If think in terms of dimensionality, the ME principle pins down a unique inversion of a projection from a high-dimensional object $e$ down to a one-dimensional scalar $r(e)$. In the machine learning literature this is known as maximum entropy pdf projection. Baggenstoss (2018) notes that “if we always choose among models that have maximum possible entropy for the given choice of features, we are likely to obtain better features and better generative models”.

The favorable performance of ME models is due simply to the fact that entropy quantifies the number of ways a particular distribution can come about, so by maximizing it we select the most likely solution presented to use by Nature. Consider the following plot of the normalized entropy of a 1000 randomly generated $e \in \mathbb{R}^{5 \times 5}$ matrices which all satisfy the constraints $\{ r(e) = 0.35,\ \sum_{ij} e_{ij}=1 \}$.

This illustrates two things: (1) many $e$ exist that satisfy the given constraints; (2) most of them lie near the maximum value $H_m$. Those that do represent distributions most likely to come about by a non-opinionated generating mechanism, often whimsically represented by a team of monkeys throwing balls in equally-sized boxes (Sivia and Skilling 2006, sec. 5.2.1). (This is essentially how statistical physics models Nature.) Our task now is to locate that $e^*$ which attains $H_m$.

Finding $e^*$

Formally, with the discrete entropy defined as

we have the constrained optimization problem

For a small amount of groups $n$ we can solve this problem numerically. Using an heuristic ansatz, we then derive an analytical solution valid for any $n$. Reproducible calculations are in this Pluto notebook.

Numerical solution

Constraining $r$ amounts just to a quadratic constraint, since

which is a quadratic constraint in the $e_{ij}$. Unfortunately, the problem is not a convex one, because the associated quadratic form is nondefinite (quadratic constraints are nonconvex, unlike quadratic inequalities). In other words, we cannot transform this entropy maximization problem into the exponential cone which would give us the global optimum.

Nevertheless, nothing stops us from looking for locally stationary points. The JuMP optimizer returns this solution for $n=5$ and $r^* := 0.35$, for example:

 5×5 Matrix{Float64}:
 0.096  0.026  0.026  0.026  0.026
 0.026  0.096  0.026  0.026  0.026
 0.026  0.026  0.096  0.026  0.026
 0.026  0.026  0.026  0.096  0.026
 0.026  0.026  0.026  0.026  0.096

Despite the fact that we assumed nothing about symmetry of $e^*$, we get back very simple solutions that (1) are symmetric and (2) look like a linear combination of I = eye(n,n) and J = ones(n,n) matrices, which we exploit below. Note that this is still true for $r < 0$.

Heuristic solution

The heuristic says that $e^*$ be a convex combination of $I$ and $J$ (the $n \times n$ identity and ones matrix), normalized such that $\sum_{ij} e_{ij} = 1$. In other words,

with $t \in [0,1]$, $n$ the number of discrete classes and $I$ is the $n \times n$ identity matrix and $J$ the $n \times n$ all‑ones matrix. This heuristic linearly interpolates the solutions for two limiting cases:

1. $r=0 \Longrightarrow e^*=J/n^2$: edges spread uniformly over all group pairs (no assortativity)
2. $r=1 \Longrightarrow e^*=I/n$: all edges strictly within groups (perfect assortativity)

Now we can plug this in $r(e)$ and solve for $r$. This yields

such that

which is indeed the simplest possible form one would expect, and which agrees with the numerical solution obtained with JuMP shown above (and does so for any value of $(n, r^*)$ I could test numerically). The expressions for $a_i = b_i = 1/n$ are constant: the sums along rows and columns always add up to $1/n$; whereas the trace $\text{Tr}[e(r)] = r + (1-r)/n$ does depend on $r$.

Is this the global solution?

The entropy difference (Jaynes 2003, 287) of $e^*(r)$ is given by

where $H_m = \log n^2$ is the maximum possible value of the entropy and $f(x) = x \log x$. In general, the entropy difference quantifies the difficulty of generating valid candidate distributions, and therefore the strength of the applied constraints.

This last plot shows that for $r = 0$ the heuristic solution $e^*(r=0)$ is indeed optimal, since we have reached the maximum possible value of the entropy $H_m(n)$ while satisfying the constraints.

The optimal ME solution is smooth in $r$. If we assume that it is unique, then intuition suggests that our heuristic is in fact that unique solution, since it goes smoothly into the known optimal solution as $r \rightarrow 0$. It is probably possible to show this rigorously: please reach out if you have an idea on how to do so!

Sampling vs. growing networks with a given $r^*$

Now we have a defensible choice of $e$ given $r^*$, we can use eg. the algorithm in (Newman 2003, sec. IIC) to sample a network that will tend to $e^*(r^*)$ and therefore to $r^*$ asymptotically.

However, it might be more desirable to use a growing method, because this has the advantage that it can be used in an on-line fashion — growing networks by adding one or more edges per timestep, as is usually done in dynamical ABM simulations.⁶ A straightforward growing method is:

1. Sample a pair $(i,j) \sim e^*_{ij}$
2. Sample a node (agent) uniformly from group $i$
3. Sample a node (agent) uniformly from group $j$
4. Connect the two sampled nodes (agents) from steps 2 and 3
5. Repeat for each timestep

This might be the simplest possible way to achieve this, and would be probably what one would come up with after a moment’s thought. And indeed, this algorithm is itself equivalent to a maximum entropy model known as the Poisson model (Peixoto 2020 A.1), which is a ME solution to the group-membership constraint. Therefore, we may eliminate another round of design choices when growing the interaction networks during our simulations.

Note that $r^* <$0 is fully allowed. The method can thus be used to grow disassortative networks equally well as assortative networks. This might come in handy at times since “disassortativity [in degree] is the natural state for all networks” (Newman and Park 2003).

Conclusion

In ABM, design choices are unavoidable, but whenever possible we should make them according to the maximum entropy (ME) principle: constrain only what we genuinely know and remain agnostic about everything else.⁷

I proposed such an agnostic way to sample or grow assortative networks. This may be used in ABM simulations of social networks such as Mudd et al. (2022). Assortative networks are of great interest in the social sciences, as are questions of causality, and in investigating these murky waters our ABMs can do with every bit of bias removal the ME principle affords them.

Go to next post ▤ in research series.